Insecurely encrypting images with Rust
This article demonstrates how a block encryption cipher can still be insecure if it uses an insecure mode of operation. It includes a simple Rust program that encrypts PPM images using the AES block cipher with different modes of operation.
A primer on encryption
In the simplest possible terms, encryption is achieved by taking an input (in our case an image), applying some operations to it, and producing an output that differs from the original input, with the purpose of protecting data from prying eyes. Crucially, the output must be reversible, so that the original input can be recovered.
Scrambling the original input to produce an encrypted output is achieved through a key, which is a sequence of bytes. In the case of symmetric encryption, the output can only be decrypted by using the same key that was used to encrypt it.
This is different from asymmetric encryption (also known as public-key encryption), where the key used for encryption is different from the key used for decryption. The modern internet relies on asymmetric encryption: as a matter of fact, you're reading this blog post over HTTPS, which means your browser and the server participated in a key exhange mechanism. That exchange produced a shared symmetric key which was then used to encrypt the HTTP traffic.
For the purpose of this blog post, I'll be focusing on symmetric encryption.
Block ciphers and modes of operation
Aumasson defines a block cipher as consisting of an encryption algorithm E which takes a key K and a plaintext P as its input, and produces a ciphertext C. That is to say, encryption is expressed as C = E(K, P), and decryption as its inverse, i.e. P = D(K, C)
A block cipher is so named because it operates on fix-sized blocks. AES (Advanced Encryption Standard) is the most popular block cipher, and it processes data in blocks of 16 bytes at a time. If the input length is not divisible by 16, the remainder is usually padded.
How should the cipher behave when encrypting some arbitrarily sized input? This is when modes of operation come into play. A mode of operation provides instructions on what to do on long sequences of input.
The most intuitive, and probably the most problematic (we'll see why in a bit), is the Electronic Code Book (ECB) mode of operation. ECB simply applies the encryption algorithm to a block, then proceeds to applying it to the next block and so on, until the plaintext is fully exhausted.
Plaintext Plaintext Plaintext
↓ ↓ ↓
+-------------+ +-------------+ +-------------+
Key →| AES | Key →| AES | Key →| AES |
+-------------+ +-------------+ +-------------+
↓ ↓ ↓
Ciphertext Ciphertext Ciphertext
One of the security goals of encryption is indistiguishability from random data, but encrypting blocks is fundamentally at odds with that goal, because it reveals patterns from the original plaintext. Think of it this way: if the same block is encrypted twice, it will produce exactly the same output. You may not figure out what that means, but you'll still get enough details about the plaintext which you were trying to hide in the first place.
The most striking example that has been used over the years to drive home this point is the infamous ECB Penguin: even after encrypting an image of the Linux mascot using AES-ECB, you can still see the penguin!
| Original image | Encrypted with AES-ECB |
|---|---|
 |  |
I decided to write a small Rust program to achieve the same result and demonstrate that even using a 256-bit long key derived with the state-of-the-art Argon2 password-hashing algorithm, ECB still proves to be insecure.
The PPM format
Filippo Valsorda cleverly pointed out that the easiest image format to manipulate to achieve this is PPM, or Portable Pixel Map. This is because the format is very easy to parse, and only consists of the following:
- A magic number at the beginning of the file
- The width of the image
- The height of the image
- The highest byte value in the image content
- A raster of height rows, in order from top to bottom (these are raw bytes if the magic number is
P6, or ASCII characters if the magic number isP3)
Here is an example of a plain PPM file:
P3 # This is the magic number denoting a plain PPM file
4 4 # The width and the height of the image
15 # The maximum byte size, followed by the raster
0 0 0 0 0 0 0 0 0 15 0 15
0 0 0 0 15 7 0 0 0 0 0 0
0 0 0 0 0 0 0 15 7 0 0 0
15 0 15 0 0 0 0 0 0 0 0 0
Conveniently, the format supports # comments, which will come in handy later.
Let's get parsing
The idea is to leave the header portion of the file intact, and to encrypt only the actual data. This lets us open the image and view it - if we were to encrypt the entire file, that would also include the header, meaning your computer will have a hard time understanding what kind of file it is.
Let's model the structure:
#[derive(Debug)]
pub enum MagicNumber {
/// Indicates ASCII data
P3,
/// Indicates binary data
P6,
}
#[derive(Debug)]
pub struct PpmHeader {
magic_number: MagicNumber,
pub width: usize,
pub height: usize,
pub max_val: usize,
pub end: usize,
}
#[derive(Debug)]
pub struct Ppm {
pub header: PpmHeader,
pub data: Vec<u8>,
}
I've included end to keep track of the offset delimiting the end of the header.
Now we'll want to add some parsing logic for the header:
impl PpmHeader {
pub fn from_str(text: &str) -> color_eyre::Result<Self> {
let mut tokens = text
.lines()
.filter_map(|line| {
let line = line.trim();
if line.starts_with('#') {
None
} else {
Some(
line.split_whitespace()
.take_while(|token| !token.starts_with('#')),
)
}
})
.flatten();
let magic_number =
MagicNumber::from_str(tokens.next().ok_or_else(|| eyre!("Missing identifier"))?)?;
// More parsing...
Ok(PpmHeader {
magic_number,
width,
height,
max_val,
end,
})
}
}
And putting it all together, i.e. parsing the whole file including header and data:
impl Ppm {
pub fn from_file(file: impl AsRef<Path>) -> color_eyre::Result<Self> {
let mut file = File::open(file)?;
let mut buffer = Vec::new();
file.read_to_end(&mut buffer)?;
// Turn the bytes into text
let image_text = String::from_utf8_lossy(&buffer);
// Parse the header
let header = PpmHeader::from_str(&image_text)?;
let start_offset = image_text[header.end..]
.find(|c: char| !c.is_whitespace())
.map(|i| header.end + i)
.ok_or_else(|| eyre!("Could not find start of pixel data"))?;
let data = match header.magic_number {
// Deserialize the data: if the magic number is P3, split by whitespace
// and parse each number into an unsigned 8-bit integer
MagicNumber::P3 => {
let ascii_data = &image_text[start_offset..];
ascii_data
.split_whitespace()
.map(|s| s.parse::<u8>())
.collect::<Result<Vec<u8>, _>>()?
}
// Otherwise, if the magic number is P6, store the raw bytes
MagicNumber::P6 => buffer[start_offset..].to_vec(),
};
Ok(Ppm { header, data })
}
}
So far so good. This allows us to call Pnpm::from_file and have a struct holding the header and the actual byte data of the image.
let mut image = Ppm::from_file(&file)?;
Encrypting with a user-provided passphrase
AES requires a key of 128-bytes for its encryption algorithm, though you could also use variants of AES that accept longer keys. Ask any human to produce a key of that length, and you'll be met with a blank stare. Fortunately, password-based key derivation functions exist: given a password, they produce a sequence of bytes which can be used as an encryption key.
Given how insecure ECB is, you may be tempted to think that using a really strong key, generated with a sophisticated key derivation function, might provide enough security. You'd be sorely mistaken.
Let's see why that is the case. I've picked Argon2 for this example, which is widely considered one of the best password-hashing functions due to its properties (memory hardness, among others). It requires a salt as part of the input, so that two encryption keys derived from the same passphrase (but crucially, from two different salts) result in different outputs.
// Create a 16-byte-long buffer, which is Argon2's recommended length for a salt
let mut salt = [0u8; Salt::RECOMMENDED_LENGTH];
// Fill the buffer with random bytes from the operating system
OsRng.fill_bytes(&mut salt);
// Create a 32-byte buffer to use as the encryption key
let mut output_key_material = [0u8; 32];
// ...and fill it with bytes created by the Argon2 function using
// "i-have-eaten-the-plums-that-were-in-the-icebox" as the passphrase,
// which is arguably more memorable than a sequence of 32 random-looking bytes
Argon2::default()
.hash_password_into(b"i-have-eaten-the-plums-that-were-in-the-icebox", &salt, &mut output_key_material)
.unwrap();
We now have all the elements to encrypt our penguin. Let's add a method to the Ppm implementation:
impl Ppm {
// ...other methods
/// Encrypts the data using AES256-ECB.
/// For demonstration purposes only!
pub fn encrypt_with_aes_ecb(&mut self, cipher: &Aes256) {
const BLOCK_SIZE: usize = 16;
let padding = BLOCK_SIZE - (self.data.len() % BLOCK_SIZE);
self.data.extend(vec![padding as u8; padding]);
for chunk in self.data.chunks_exact_mut(BLOCK_SIZE) {
cipher.encrypt_block(GenericArray::from_mut_slice(chunk));
}
}
}
As indicated by &mut self in the signature, this will mutate the original data stored in the struct.
All that's left to do is writing a function to dump the bytes to disk:
impl Ppm {
// ...other methods
pub fn write_to_disk(&self, path: &Path) -> color_eyre::Result<()> {
let mut buf: Vec<u8> = Vec::new();
writeln!(&mut buf, "{}", MagicNumber::P6)?;
writeln!(&mut buf, "{} {}", self.header.width, self.header.height)?;
writeln!(&mut buf, "{}", self.header.max_val)?;
buf.extend_from_slice(&self.data);
fs::write(&path, &buf)?;
Ok(())
}
}
And here is the result...

Even with a 256-bit key generated with Argon2, AES-ECB is still insecure. You can stil see the penguin.
What about decryption?
We could stop here, but let's write a decryption function for the sake of completeness.
You will recall that a successful decryption can only occur if the same encryption key is used for decryption. However, the Argon2-derived key was generated with a random salt, and the same salt must be used in order to produce the same key. This means the salt must be stored somewhere. What better place than the PPM file header itself?
The PPM format conveniently allows comments in the header: anything following the # character is treated as a comment.
We can leverage that to our advantage by storing the salt in the header, and updating the Rust code accordingly when reading from/writing to disk.
#[derive(Debug)]
pub struct PpmHeader {
magic_number: MagicNumber,
pub width: usize,
pub height: usize,
pub max_val: usize,
pub end: usize,
// Store the salt here
pub salt: Option<Vec<u8>>,
}
Storing the salt as part of the file is not a security risk. In fact, SQLCipher, an encrypted version of SQLite, stores the salt as the first 16 bytes of the database file! Note that I chose to represent the salt bytes in hexadecimal notation, but any encoding will do.
$ head -n4 Tux.encrypted.ppm
P6
265 314
# salt a35211ebcbc5ccca063910c61d54deaa
255
All of this is useless, ECB is still bad! Can we do better?
We can use GCM instead. GCM stands for Galois/Counter Mode, and effectively turns the block cipher into a stream cipher.
The math behind GCM is very complicated, but it comes with extremely useful properties: it uses a counter internally, meaning that the same block encrypted twice will produce a different result. This conveniently solves the pattern leakage issue that ECB suffers from.
It also provides authenticated encryption, which is an encryption scheme that makes the ciphertext tamper-resistant. It achieves this by producing an authentication tag, so that the integrity of the message is also verified during decryption. In other words, if any bytes of the ciphertext bytes were altered, decryption would not succeed.
This makes it an ideal candidate for a large number of use cases. Chances are you've been using AES-GCM without even realising. AWS, for example, uses it to encrypt S3 files at rest, and it's also commonly used in Wi-Fi communication protocols. Generally speaking, AES is so ubiquitous that modern CPUs include special instructions to perform its operations as quickly and efficiently as possible.
Let's put it to the test. AES-GCM requires a nonce (number used once) to produce a unique keystream. We'll also need to keep track of the nonce for decryption purposes, so let's change the structure of our PPM header:
#[derive(Debug)]
pub struct PpmHeader {
magic_number: MagicNumber,
pub width: usize,
pub height: usize,
pub max_val: usize,
pub end: usize,
pub salt: Option<Vec<u8>>,
// Let's store the nonce here
pub nonce: Option<Vec<u8>>,
}
Of course, we still need to generate an encryption key; we can derive one with Argon2, as above.
let mut salt = [0u8; Salt::RECOMMENDED_LENGTH];
OsRng.fill_bytes(&mut salt);
image.header.salt = Some(salt.to_vec());
let mut output_key_material = [0u8; 32];
Argon2::default()
.hash_password_into(key.as_bytes(), &salt, &mut output_key_material)
.unwrap();
let cipher = Aes256Gcm::new(&GenericArray::from_slice(&output_key_material));
image.encrypt_with_aes_gcm(&cipher)?;
And here is the encrypt_with_aes_gcm function:
impl Ppm {
// ...other methods
pub fn encrypt_with_aes_gcm(&mut self, cipher: &Aes256Gcm) -> color_eyre::Result<()> {
let nonce = Aes256Gcm::generate_nonce(&mut OsRng);
self.header.nonce = Some(nonce.to_vec());
let ciphertext = cipher
.encrypt(&nonce, self.data.as_slice())
.map_err(|e| eyre!("AES-GCM encryption error: {:?}", e))?;
self.data = ciphertext;
Ok(())
}
}
| Original image | Encrypted with AES-ECB | Encrypted with AES-GCM |
|---|---|---|
 |  | 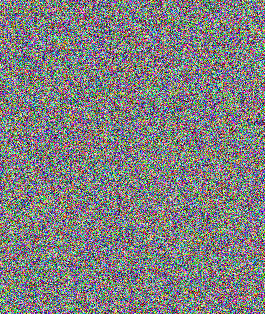 |
Conclusions
The image encrypted with AES-GCM bears no resemblance to the original input. The big white, black, and orange blobs of colour are clearly distinguishable when using AES in ECB mode, despite having used a state-of-the-art encryption key derivation function. Ultimately, ECB transforms the blocks from the original input in an extremely predictable way, making the encryption key almost laughably irrelevant.
On the other hand, it is impossible to spot any element of the original image in the GCM output: the penguin disappeared.
Notes
The Tux.ppm image and the CLI source code are available for download.
Below are some extra checks validating the integrity of the files after the encryption/decryption round trip.
# Round trip with AES-ECB produces the same digest
cargo run -- encrypt --file Tux.ppm --key sunshine123 --mode ecb
cargo run -- decrypt --file Tux.Ecb.67438efc.encrypted.ppm --key sunshine123 --mode ecb
sha256 Tux.ppm # 6fb56d4eb39e35603b525e9dd3e3cd33a16e34f32bd1196ae47402df65a50ab0
sha256 Tux.Ecb.67438efc.decrypted.ppm # 6fb56d4eb39e35603b525e9dd3e3cd33a16e34f32bd1196ae47402df65a50ab0
# Round trip with AES-GCM also produces the same digest
cargo run -- encrypt --file Tux.ppm --key sunshine123 --mode gcm
cargo run -- decrypt --file Tux.Gcm.f56ef398.encrypted.ppm --key sunshine123 --mode gcm
sha256 Tux.Gcm.f56ef398.decrypted.ppm # 6fb56d4eb39e35603b525e9dd3e3cd33a16e34f32bd1196ae47402df65a50ab0